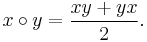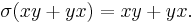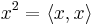Jordan algebra

In abstract algebra, a Jordan algebra is an (not necessarily associative) algebra over a field whose multiplication satisfies the following axioms:

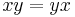  1. xy = yx (commutative law)
  2. (xy)(xx) = x(y(xx)) (Jordan identity).

The product of two elements x and y in a Jordan algebra is also denoted x ∘ y, particularly to avoid confusion with the product of a related associative algebra.

Jordan algebras were first introduced by Pascual Jordan (1933) to formalize the notion of an algebra of observables in quantum mechanics. They were originally called "r-number systems", but were renamed "Jordan algebras" by Albert (1946), who began the systematic study of general Jordan algebras.

Contents

Special Jordan algebras

Given an associative algebra A (not of characteristic 2), one can construct a Jordan algebra A+ using the same underlying addition vector space. Notice first that an associative algebra is a Jordan algebra if and only if it is commutative. If it is not commutative we can define a new multiplication on A to make it commutative, and in fact make it a Jordan algebra. The new multiplication x ∘ y is as follows:

x\circ y = {xy%2Byx \over 2}.

This defines a Jordan algebra A+, and we call these Jordan algebras, as well as any subalgebras of these Jordan algebras, special Jordan algebras. All other Jordan algebras are called exceptional Jordan algebras. The Shirshov–Cohn theorem states that any Jordan algebra with two generators is special. Related to this, Macdonald's theorem states that any polynomial in three variables, which has degree one in one of the variables, and which vanishes in every special Jordan algebra, vanishes in every Jordan algebra.

Hermitian Jordan algebras

If (A, σ) is an associative algebra with an (anti-)involution σ, then if σ(x)=x and σ(y)=y it follows that

\sigma(xy %2B yx) = xy %2B yx.

Thus the set of all elements fixed by the involution (sometimes called the hermitian elements) form a subalgebra of A+ which is sometimes denoted H(A,σ).

Examples

1. The set of self-adjoint real, complex, or quaternionic matrices with multiplication

(xy %2B yx)/2

form a special Jordan algebra.

2. The set of 3×3 self-adjoint matrices over the non-associative octonions, again with multiplication

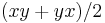(xy %2B yx)/2,

is a 27 dimensional, exceptional Jordan algebra. Its automorphism group is related to the exceptional Lie group F₄. Since over the real numbers this is the only exceptional Jordan algebra, it is often referred to as "the" exceptional Jordan algebra. It was the first example of an Albert algebra.

Derivations and structure algebra

A derivation of a Jordan algebra A is an endomorphism D of A such that D(xy) = D(x)y+xD(y). The derivations form a Lie algebra der(A). The Jordan identity implies that if x and y are elements of A, then the endomorphism sending z to x(yz)−y(xz) is a derivation. Thus the direct sum of A and der(A) can be made into a Lie algebra, called the structure algebra of A, str(A).

A simple example is provided by the Hermitian Jordan algebras H(A,σ). In this case any element x of A with σ(x)=−x defines a derivation. In many important examples, the structure algebra of H(A,σ) is A.

Derivation and structure algebras also form part of Tits' construction of the Freudenthal magic square.

Formally real Jordan algebras

A (possibly nonassociative) algebra over the real numbers is said to be formally real if it satisfies the property that a sum of n squares can only vanish if each one vanishes individually. In 1932, Pascual Jordan attempted to axiomatize quantum theory by saying that the algebra of observables of any quantum system should be a formally real algebra which is commutative (xy = yx) and power-associative (the associative law holds for products involving only x, so that powers of any element x are unambiguously defined). He proved that any such algebra is a Jordan algebra.

Not every Jordan algebra is formally real, but Jordan, Neumann & Wigner (1934) classified the finite dimensional formally real Jordan algebras. Every formally real Jordan algebra can be written as a direct sum of so-called simple ones, which are not themselves direct sums in a nontrivial way. In finite dimensions, the simple formally real Jordan algebras come in four infinite families, together with one exceptional case:

where the right-hand side is defined using the usual inner product on Rn. This is sometimes called a spin factor or a Jordan algebra of Clifford type.

Of these possibilities, so far it appears that nature makes use only of the n×n complex matrices as algebras of observables. However, the spin factors play a role in special relativity, and all the formally real Jordan algebras are related to projective geometry.

Generalizations

Infinite dimensional Jordan algebras

In 1979, Efim Zelmanov classified infinite dimensional simple (and prime) Jordan algebras. They are either of Hermitian or Clifford type. In particular, the only exceptional simple (and prime) Jordan algebras are finite dimensional Albert algebras, which have dimension 27.

Jordan rings

A Jordan ring is a generalization of Jordan algebras, requiring only that the Jordan ring be over a general ring rather than a field. Alternatively one can define a Jordan ring as a commutative nonassociative ring that respects the Jordan identity.

Jordan superalgebras

The Jordan superalgebras over an algebraically closed field of characteristic 0 were classified by Kac (1977). They include several families and some exceptional algebras notably 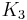K_3 and K_{10}

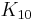
Peirce decomposition

If e is an idempotent in a Jordan algebra A (e2=e) and R is the operation of multiplication by e, then

so the only eigenvalues of R are 0, 1/2, 1. If the Jordan algebra A is finite-dimensional over a field of characteristic not 2, this implies that it is a direct sum of subspaces A = A0(e) ⊕ A1/2(e) ⊕ A1(e) of the three eigenspaces. This decomposition was introduced by Albert (1947) and is called the Peirce decomposition of A relative to the idempotent e.

See also

References